Fuzzy search dictionary universal machine Levenshtein. Part 2

first article we considered the universal Levenshtein automaton is a powerful tool to filter the words that are separated by some word W on the Levenshtein distance is not a given. Now it's time to explore ways of using this tool for the effective solution of the problem of fuzzy search in the dictionary.

The easiest and most obvious algorithm for solving the problem of fuzzy search using Levenshtein automaton — algorithm for complete enumeration. In this case, for each word in the dictionary evaluated the Levenshtein distance (Arnulf-Levenshtein) to the search query. Example implementation in C#, you can look at first article.

The use of even this simple algorithm gives a performance benefit compared to the use of dynamic programming methods. However, there are more efficient algorithms.

the

the Basic algorithm of Schulz and Mihov

Consider the first such algorithm as far as I know, he was offered Mihovil and Schultz (2002), so I'll call it the basic algorithm of Schulz and Mihov or just base. So, even for a supposedly distorted words W and threshold edit-distance N is specified a deterministic automaton Levenshtein A_N(W). Let consider a dictionary D is also represented as a deterministic finite state machine A_D that has an input alphabet E. State machines will be denoted as q and q^D accordingly, the function of transitions as V and V^D and the final state set as F and F^D. Proposed by Schultz and Mihovil fuzzy search algorithm in the dictionary is a standard procedure backtracking and can be described by the following pseudocode:

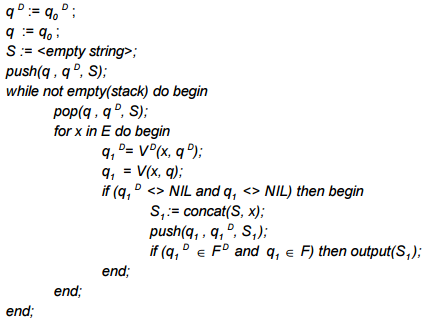
The algorithm starts with the initial States of the automata. As of the filing of the entry of new characters, stacked subsequent state unless they are empty. If the next state of both automata are finite — discovered the word.

This algorithm can still be represented as an intersection of finite automata. In the sample output only those words which correspond to final States of both machines. By considering only the prefixes that translate both the machine in non-empty state.

The computational complexity of the algorithm depends on the size of the dictionary and edit-distance N. If N reaches the size of the longest word in the dictionary, the algorithm boils down to the complete enumeration of States in the automaton is A_D. But in solving practical problems, as a rule, used small N. In this case, the algorithm considers only a very small subset of States in the automaton is A_D. When N=0, the algorithm finds the dictionary, the word W during O(|W|).

It is worth noting that the described algorithm ensures no loss during the search. That is, 100% of the words in the dictionary, separated from the W within N you will get in the sample output.

the

software implementation

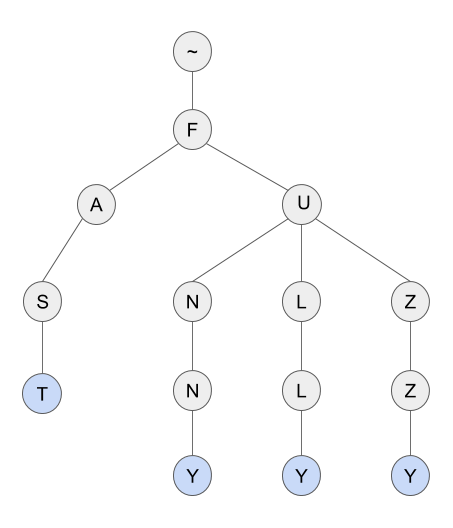
I assume you are already familiar with this data structure as the prefix tree. The prefix tree is also known as “loaded tree” (or “forest”, “ray”, “Trie”) and successfully used for the storage of dictionaries. The figure shows the prefix tree for the vocabulary of four words: “fast”, “funny”, “fully”, “fuzzy”.

If you are not familiar with the prefix tree, we can find publications in which this structure is discussed in detail, for example, here.

Why I want to use to store the dictionary prefix tree? Because the prefix tree can be viewed as a finite automaton. Each tree node represents a state machine. The initial state is the root of the tree, and the end States of the nodes corresponding to the words. For each node, and the symbol is only one possible transition automaton is deterministic.

So looking at the prefix tree as a deterministic finite state machine and having a software implementation of a deterministic Levenshtein automaton, it is easy to transform the pseudocode into code in any programming language. Under spoiler an example in C#.

Basic

/// <summary>
/// Find all words in dictionary such that Levenstein distance to typo less or equal to editDistance
/// </summary>
/// <returns>the Set of possible corrections</returns>
/// <param name="typo">Garbled word.</param>
/// <param name="dictionary" > Dictionary.</param>
/// <param name="editDistance">Edit distance.</param>
IEnumerable<string> GetCorrections(typo string, TrieNode dictionary, int editDistance) { 
var corrections = new List<string> (); 
if (string.IsNullOrEmpty (typo.Trim())) {
return corrections;
} 
//Create automaton
LevTAutomataImitation automaton = new LevTAutomataImitation (typo, editDistance);
//Init the stack with the start states
Stack<TypoCorrectorState> stack = new Stack<TypoCorrectorState> ();
stack.Push (new TypoCorrectorState () {
Node = dictionary,
AutomataState = 0,
AutomataOffset = 0,
});
//Traversing trie with standard backtracking procedure
while (stack.Count > 0) {
//State to process
TypoCorrectorState state = stack.Pop();
automaton.LoadState (state.AutomataState, state.AutomataOffset);
//Iterate over TrieNode children
foreach (char c in state.Node.children.Keys) {
//Evaluate state of Levenstein automaton for given letter
int vector = automaton.GetCharacteristicVector (c, state.AutomataOffset);
AutomataState nextState = automaton.GetNextState (vector);
//If next state is not  empty  state
if (nextState != null) {
TrieNode nextNode = state.Node.children [c];
//Push node and automaton state to the stack
stack.Push (new TypoCorrectorState () {
Node = nextNode,
AutomataState = nextState.State
AutomataOffset = nextState.Offset
});
//Check if word with Levenstein distance <= n found
if (nextNode.IsWord && automaton.IsAcceptState (nextState.State, nextState.Offset)) {
corrections.Add (nextNode.Value);
}
}
} 
}
return corrections;
}

the

Algorithm FB-Trie

Go ahead. 2004 Mihov and Schulz suggested a modication of the above algorithm whose main idea is to use the forward and reverse prefix tree combined with a partitioning of the search query W into two approximately equal parts W₁ and W₂. The algorithm known under the name FB-Trie (trie forward and backward).

Under the reverse prefix tree it is necessary to understand the prefix tree constructed by the inversions of all of the vocabulary words. Inversion of words I call a word spelled backwards.

Important point — the work of Mihov and Schulz showed that the distance of the Arnulf-Levenshtein inversions between the two strings is equal to the distance between the lines.

The algorithm for N=1 is based on the following statement: any string S, which is separated from the string W at a distance, Arnulf-Levenshtein d(S, W) <= 1, it is possible to separate the two parts of S₁ and S₂ only to satisfy one of three mutually exclusive conditions is true:

a) d(S₁, W₁) = 0 and d(S₂, W₂) <= 1

b) d(S₁, W₁) <= 1 and d(S₂, W₂) = 0

C) d(S₁, W₁’) = 0 and d(S₂, W₂’) = 0

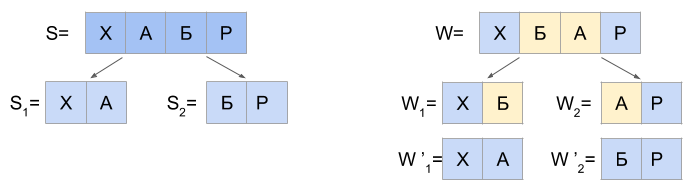
In the “to” line W₁’ and W₂’ is derived from lines W₁ and W₂ by replacing the last character W₁ to the first character W₂ and Vice versa. For example, if W₁=’FU’ while W₂=’ZZY’, then W₁’=’FZ’ and W₂’=’UZY’.

How you can quickly find in the dictionary all words that fit the “a”? Very easy to find in the prefix tree node with the prefix W₁, then to avoid all his heirs in accordance with the basic algorithm of Schulz and Mihov and select those keys which are separated from W₂ at a distance of not more than 1.

option a

//May be for some S d(S1, W1) = 0 and d(S2, W2) <= 1?
TrieNode lnode = ForwardDictionary.GetNode (left);
if (lnode != null) {
corrections.AddRange(GetCorrections(right, lnode, 1));
}

For option “b” will be useful for the reverse prefix tree: find the node corresponding to the inverted line W₂, then move around all of his heirs and will select those keys which are spaced from the inverted W₁ at a distance of not more than 1, again in accordance with the basic algorithm.

Option B

//May be for some S d(S1, W1) = 1 and d(S2, W2) = 0?
TrieNode rnode = BackwardDictionary.GetNode (rright);
if (rnode != null) {
corrections.AddRange(GetCorrections(rleft, rnode, 1))));
}

For option “V” you just need to swap two characters in the word W on the division boundary and check to see if the prefix tree resulting word.

Option

//May be there is a transposition in the middle?
char[] temp = typo.ToCharArray ();
char c = temp [llen - 1];
temp [llen - 1] = temp [llen];
temp [llen] = c;

TrieNode n = ForwardDictionary.GetWord (new string(temp));
if (n != null) {
corrections.Add (n.Key);
}

To solve the problem of fuzzy search algorithm FB-Trie, you just need to find three of the above set of words and combine them.

For N=2 need to consider two cases more:

a) d(S₁, W₁) = 0 and d(S₂, W₂) <= 2

b) 1 <= d(S₁, W₁) <= 2 and d(S₂, W₂) = 0

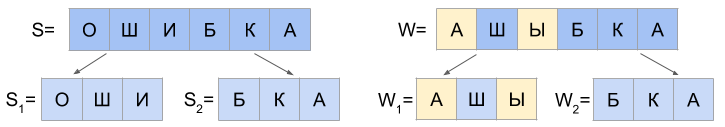
C) d(S₁, W₁) = 1 and d(S₂, W₂) = 1

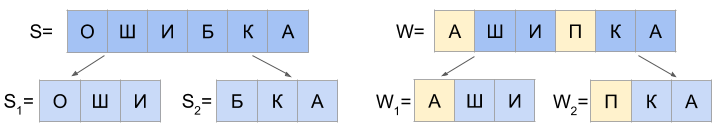
And if the last character of the string S₁ is the first character in W₂ and latest W₁ is the first character S₂, then there are two cases:

g) d(S₁, W₁’) = 0 and d(S₂, W₂’) <= 1

d) d(S₁, W₁’) <= 1 and d(S₂, W₂’) = 0

The first two cases are easily detected by analogy with the variants “a” and “b” for N=1, but use the machine for Levenshtein N=2.

Options “g” and “d” for N=2 repeat options “a” and “b” for N=1, only instead of substrings W₁ and W₂ used W₁’ and W₁’.

The variant is slightly more complicated. The first step is to find in direct of the prefix tree, all nodes corresponding to the prefixes, which are separated from W₁ at a distance of not more than 1 (basic algorithm). In the second step, for each such node must be crawled subsidiaries and to select those that correspond to keys that are separated from W₂ at a distance of not more than 1 (again, the underlying algorithm).

For N=3 will need to consider seven cases. Bring them here will not — can view the original article Mihova and Schultz (2004). By analogy, you can continue to an arbitrary N, although the need for this at the decision of practical tasks is unlikely to arise.

the

performance Evaluation

Interestingly, the search time using the algorithm of the FB-Trie decreases with increasing the length of the word W.

A detailed analysis of the search time using an algorithm FB-Trie compared with other widely known algorithms of fuzzy search can be found in the work of Leonid Boytsov “Indexing Methods for Approximate Dictionary Searching: Comparative Analysis” (2011). The work offers a detailed comparison of search time and memory consumption for these algorithms as:

the

exhaustive;
various modifications of the method n-grams;
various modifications of the method of expanding a selection;
hashing for signature;
FB-Trie and other algorithms.

I will not repeat here all of the many figures and graphs, but limited to only General conclusions to natural languages.
So, the algorithm FB-Trie provides a reasonable compromise between performance and memory consumption. If your application task is required to support the edit distance of 2 or more, and dictionary contains over 500,000 words — the algorithm FB-Trie rational choice. It will provide a minimal search time at a reasonable memory consumption (about 300% of the amount of memory occupied by the vocabulary).

If you have decided to limit the edit distance N=1, or you have a small dictionary, some algorithms can run faster (e.g., Mor−Fraenkel method or FastSS), but be prepared for increased memory consumption (up to 20,000% of the lexicon). If you have tens of gigabytes of RAM to store the fuzzy index, you can use these methods and the large sizes of the dictionary.

So that the reader could decide how many — 500,000 words, I will cite some figures for the number of words in Russian (taken here).

Spelling dictionary Lopatin contains 162,240 words — the file size of the lexicon 2 MB.
the List of names includes at least 247,780 names — the file size of 4.6 MB lexicon.
Full accentuation paradigm of the Russian language by A. A. Zaliznyak is 2,645,347 word forms, the file size of the lexicon about 35МБ.

What if you are not able to store the dictionary in the form of two prefix trees? For example, he is represented as a sorted list. In this case, the use of the machine Levenshtein for fuzzy search possible, but impractical. Possibly because there are various modifications of full search (for example, by trimming the length of the word |W| plus or minus N). Impractical — because you will not get a gain in performance compared to more simple to implement methods (for example, algorithm extensions sample).

Note that the underlying algorithm of Schulz and Mihov requires two times less memory than the algorithm of the FB-Trie. However, it will have to pay the increase in search time by an order (the authors of the algorithm).

The consideration of algorithms of fuzzy search using Levenshtein automaton is complete.

Yes, full source code Spellchecker-and C# can be found here. Perhaps my implementation is not optimal from the performance point of view, but it will help you understand the operation of the algorithm FB-Trie and maybe useful in solving your application problems.

Anyone who read the publication — a huge thank you for your interest.

the

Поиск по этому блогу

computer express